[Draft] A short and informal replication of Petrovich and Buonomo 2018
I recently came across a very interesting study by Eugenio Petrovich and Valerio Buonomo (2018), in which they analyze co-citation networks for the last three decades of analytic philosophy. After a bit of conversation with Eugenio, I thought that I would do a little quasi-replication of their results, to try out some things.
So I downloaded the sample Petrovich and Buonomo used from the Web of Science. It consists of the years 1985-2014 from the following five journals:
- Philosophical Review
- Nous
- Journal of Philosophy
- Mind
- Philosophy and Phenomenological Research
The question that Petrovich and Buonomo are interested in is whether analytic philosophy has become more diverse in these thirty years. There are various ways in which one could approach this question. Petrovich and Buonomo go for visual inspection, and I will try to present an approach to that later. But, first and foremost Eugenio and I were talking about formal evaluation of the co-citation graphs. In what follows I took some inspiration from Tang, Cheng, and Chen (2017) who present a recommendable longitudinal study of the digital humanities.
Transitivities
The first thing I did was to try and get the transitivities for the different samples. Transitivity is a very basic measure of how much a graph tends to cluster. It results from three times the number of triangles in the graph (in our case those triangles consist of three sources, of which each combination was co-cited at least once) divided by the number of triplets (any three sources). A fully connected graph would score 1 on this measure, while a completely unconnected graph would result in a 0. For this little exercise I will use a sliding window approach, in which I always consider 5 years together. It results in the following picture:
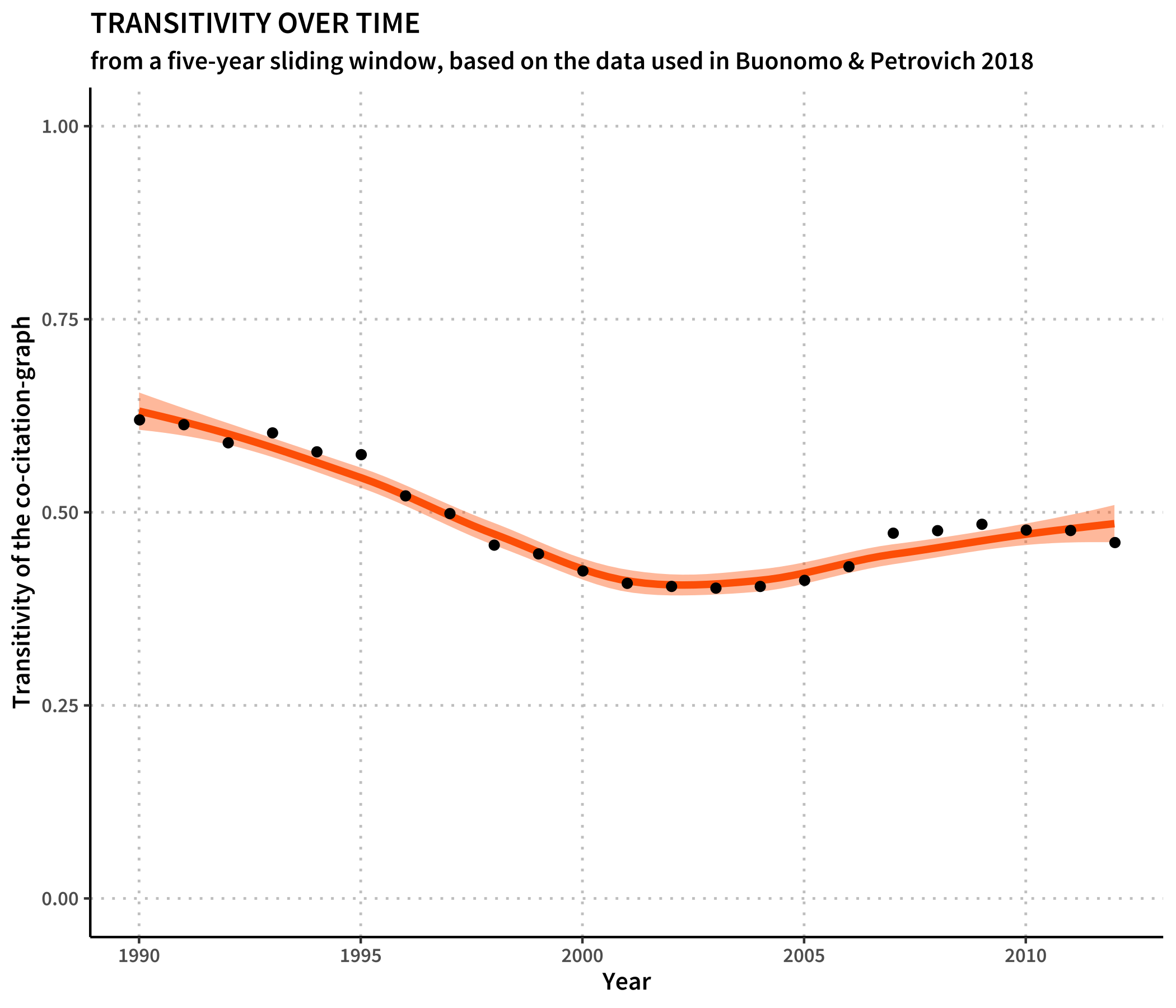
As we can see, the transitivity gets smaller over time, reaches its lowest point after 2000, and then rises again. I have also looked into the size of the so called giant component of the network, which is the largest connected sub-graph. In all cases it was higher than 93 %, and slowly approaching 98 % over time, which means that nearly all cited sources were connected via co-citation with the others. In other words: There was only one large network of philosophy, not many small unconnected sub-networks. As this was mostly constant, I think we should be able to interpret the falling transitivity as diminished local co-citation: While clusters are at the beginning very tightly knit, they get more diverse over time. We can assume that it is the local connectivity that is getting smaller, as the average minimal distance of nodes in the networks, which describes how far it usually takes to get from one randomly picked node to the next, is pretty much constant over time at 3.16 steps (std: 0.06). This value is pretty small. Short average distances together with high transitivities suggest small-world networks, in which every node can be reached from every other node via only a few steps, because the network consists of tightly clustered subunits, connected via hubs. This is a property we would generally expect from co-citation-networks drawn from one discipline. It seems to me, that we can interpret the slight diminishment of small worldedness as an indication of an increase in the scope of the kind of philosophy that appears in the surveyed journals.
Gini Coefficients
We can do another thing to get an idea about dynamics in the discipline. In some sense, citations can be considered the currency of academia. And like regular currency, some receive more, some less. Indeed, like with regular currency, a select few receive a lot more then everyone else. This suggests that we can use the same tools that are used to quantify financial inequality in societies over time to quantify inequalities in citation-counts over time. Below I have calculated the Gini-coefficients over the same five year windows used above (using a snippet by Olivia Guest). The Gini coefficient quantifies inequality on a scale from zero to one, in which zero means complete equality, while one indicates that everything is owned by only one person.
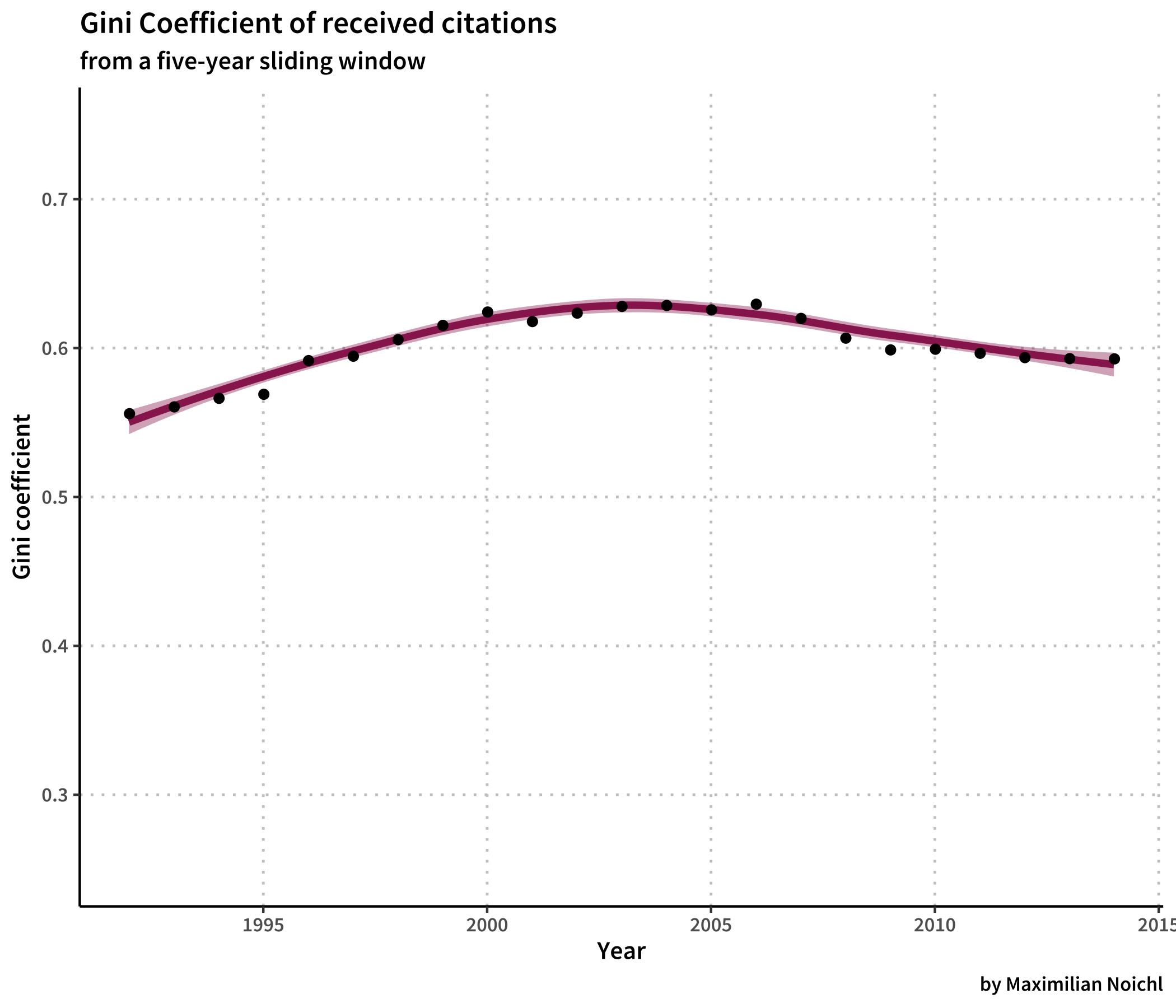
I would tend to interpret high Gini Coefficients as a sign of increased specialization, as they suggest that most articles focus on a similar set of authors. A lower gini-coefficient on the other hand might be indicative of diversification: As the circle of towering figures with very high citation-counts is enlarged, it stands to reason that also the thematic field becomes more varied. By this measure, analytic philosophy, as depicted by our sample, experienced peak specialization in the early 2000s, but has become slightly more diverse since then. This seems to be somewhat add odds with our previous result, so I’m not sure what to make of it. I would like to check this against the actual content of the articles though: Given full-texts, or at least word-vectors, it would be easy to calculate similar measures.
Visualization
Now for the most fun part, the visual inspection: A neat trick when dealing with confusing networks is to lay out their minimum spanning tree, instead of a usually zealously pruned version of the network itself. I am using the wonderful tmap-library by Probst and Reymond (2019), and will also use faerun, a visualization framework developed by the same authors. I used the Leiden-algorithm (Traag, Waltman, and van Eck (2019)) to identify communities in the networks, which are represented by the colours below.
In the networks below we see the results. Because it would be annoying to browse through 23 graphics, I will only show each of the three decades, in the same way Petrovich and Buonomo do. To read the graphics, remember that the minimum spanning tree-construction will try to put the sources with the strongest connections next to each other, which is why we have these little balls, usually around a primary source of major importance, with which all the others are co-cited. But the algorithm sometimes has to do trade-offs, so we can not expect every node to be linked to its respective nearest neighbour.
I’ve been running the YAKE-keyword algorithm on the abstracts and titles of the citing papers associated with the communities, so we can learn a little bit more about them. Be mindful, we have only titles for the first decade, which is why keyword quality here is low.
1985-1994
It’s supposed to be interactive. If it’s not´, or if the image below is too small to interact comfortably with it, maybe try it out at this link.
1995-2004
It’s supposed to be interactive. If it’s not, maybe try it out at this link.
2005-2014
It’s supposed to be interactive. If it’s not, maybe try it out at this link.
I think these graphics tend to indicate that the intellectual landscape in these five journals has been broadened over time.
Length of Bibliographies
Eugenio noted that while the sample is nearly constant over time, as the five journals output similar numbers of papers every year, the length of bibliographies, and therefore the size of the co-citation networks has increased strongly. This seems to agree with general trends in philosophy. From a larger dataset I had lying around ((used in this visualization)[https://homepage.univie.ac.at/noichlm94/full/zoom_final/index.html]) I have extracted the length of bibliographies over time, and the picture suggests quite a considerable effect (depicted using ggpointdensity{.r} by (Lukas Kremer)[https://github.com/LKremer/ggpointdensity]).
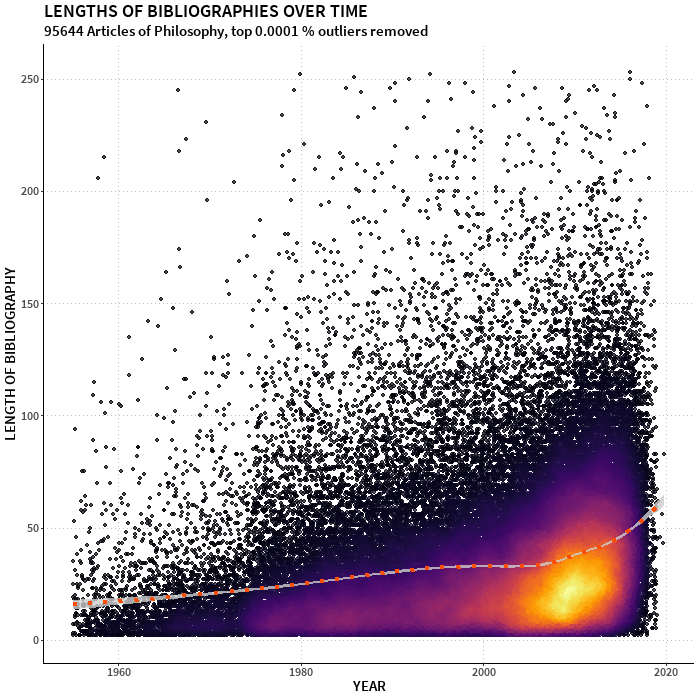
It is at the moment not clear to us what drives this effect. On the one hand, technological advancements might have made the management of large amounts of literature far easier. But it might as well be connected with various cultural changes in the discipline. I’m very interested to hear opinions on how this effect should be treated when doing diachronic analyses of literature: Should it somehow be corrected for, to ease comparability? How can it be treated a genuine feature of the data?
Literature
Petrovich, Eugenio, and Valerio Buonomo. 2018. “Reconstructing Late Analytic Philosophy. A Quantitative Approach.” Philosophical Inquiries 6 (1): 151–82. https://doi.org/10.4454/philinq.v6i1.184.
Probst, Daniel, and Jean-Louis Reymond. 2019. “Visualization of Very Large High-dimensional Data Sets as Minimum Spanning Trees”. ChemRxiv. https://doi:10.26434/chemrxiv.9698861.v1.
Tang, Muh-Chyun, Yun Jen Cheng, and Kuang Hua Chen. 2017. “A Longitudinal Study of Intellectual Cohesion in Digital Humanities Using Bibliometric Analyses.” Scientometrics 113 (2): 985–1008. https://doi.org/10.1007/s11192-017-2496-6.
Traag, V. A., L. Waltman, and N. J. van Eck. 2019. “From Louvain to Leiden: Guaranteeing Well-Connected Communities.” Scientific Reports 9 (1): 5233. https://doi.org/10.1038/s41598-019-41695-z.